Некоторые вот думают, что строки Михаила Щербакова
На честном слове или так, на отзвуке,
На первой буковке от слова честного,
Но летит он, кувыркаясь в воздухе,
По параболе Лобачевского...
суть доказательство его математической неграмотности, ибо такого
объекта не существует. Между тем, это не так.
Парабола Лобачевского есть не что иное как парабола в
плоскости Лобачевского, определенная так же, как
в обычной Евклидовой плоскости - геометрическое место точек,
равноудаленных от данной точки (фокуса параболы) и данной
прямой (директрисы параболы).
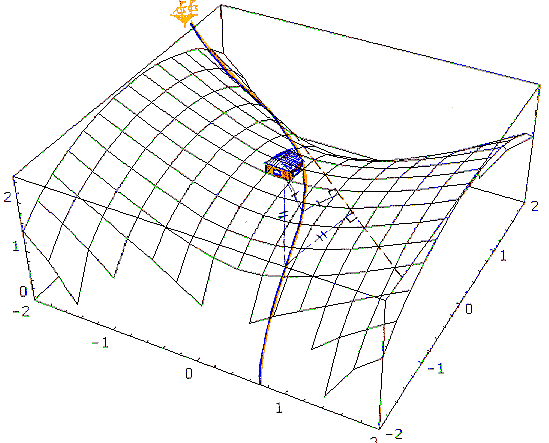
На этом рисунке изображена такая парабола для одного из частных случаев
плоскости Лобачевского (однополостного гиперболоида).
Директриса параболы отмечена
пунктиром, фокус находится в центре домика. Заметим, что поскольку
данная кривая не ограничена, то утверждение "и конца и краю нет параболе той"
также справедливо. (Насчет "края", впрочем, можно поспорить -
кривая, строго говоря, открытым множеством не является.)
Кое-кто ("пресловутый кто-то"), правда, утверждает, что, дескать, якобы
"нельзя сказать, что существует
такое математическое понятие, как парабола Лобачевского, иначе с
таким же успехом можно говорить, скажем, о "паровозе
Лобачевского" (паровоз, который находится в пространстве
Лобачевского)." Но мы (мы, кроты) дадим решительный отпор
подобного рода нездоровому критиканству и ревизионизьму.
Все, как один. Да-с.
Спасибо Юле Генюк, Леониду Цейтлину и Константину Киселеву
за напоминание некоторых
математических фактов. Буду также благодарен тому, кто нарисует
более красивую картинку вместо этой.
- Ред.
